Teoria da Regularização

Matematicamente, resolver um problema inverso significa encontrar uma solução aproximada para a equação

$$F(x) = y,$$

onde F opera entre espaços vetoriais apropriados (comumente espaços de Hilbert ou Banach). O operador F é normalmente conhecido e representa a modelagem do problema inverso em si. Em situações reais, o vetor de dados y é obtido através de medições e portanto não se pode esperar que este seja conhecido exatamente. Na prática, somente uma aproximação y^δpara y satisfazendo uma inequação do tipo

$$\|y - y^\delta\| \leq \delta$$

está disponível. Frequentemente o nível de ruídos δ > 0 é conhecido.

Um Método de Regularização é uma algoritmo capaz de resolver o problema inverso de maneira estável. Isso significa que, para cada aproximação y^δ satisfazendo a inequação acima, um método de regularização deve sempre encontrar uma aproximação x^δ para a solução do problema inversos F(x) = y de modo que, uma sequência de aproximações obtida com diferentes níveis de ruídos converge à solução exata x quando o nível de ruídos vai à zero. Isto é,

$$\lim_{\delta \rightarrow 0}x^\delta = x.$$

Principais métodos de regularização

Normalmente, os métodos de regularização se dividem em dois grandes grupos: aqueles destinados a resolver problemas lineares (quando F é um operador linear limitado) e outros mais gerais, capazes de determinar soluções aproximadas de problemas inversos não lineares.

Os métodos de regularização mais comuns são os chamados Métodos do tipo gradiente e os Métodos de Tikhonov. Para problemas não lineares, vale a pena citar também os chamados Métodos do tipo Newton.

Métodos do tipo gradiente são métodos iterativos que tentam aproximar a solução do problema inverso a partir de um chute inicial x₀. Na k-ésima iteração, o gradiente do funcional do resíduo é calculado no ponto corrente x_k e executa-se um passo do algoritmo seguindo na direção oposta ao gradiente calculado. Espera-se com isso, diminuir o resíduo do sistema linear que representa o problema inverso e eventualmente aproximar a solução desse problema. Para saber mais sobre esse tipo de método de regularização, clique aqui.

Métodos de Tikhonov são certamente os métodos de regularização mais populares. Esses métodos consistem em minimizar um funcional apropriado para encontrar uma aproximação para a solução do problema inverso. O funcional que deve ser minimizado consiste basicamente no funcional do resíduo do sistema linear que representa o problema inverso, somado a um funcional de penalização adequado para obter-se a estabilidade da solução aproximada. Para conhecer melhor o funcionamento dos métodos de Tikhonov, clique aqui.

Os métodos do tipo Newton são algoritmos iterativos utilizados para aproximar a solução de problemas inversos não lineares. Baseados no método de Newton, esses algoritmos iniciam com um chute inicial x₀. No k-ésimo passo do algoritmo, o problema inverso original é linearizado em torno do ponto corrente x_k, resultando num sistema linear, cuja solução aproximada é somada ao ponto corrente para gerar a atualização x_k+1. Clique aqui para conhecer mais sobre esses métodos.

Exemplo

Suponha que uma haste fina de comprimento igual a 1 u.m. tenha as suas duas extremidades fixadas em recipientes com gelo fundente, de modo que estas permaneçam em temperatura constante igual a zero. Se uma fonte de calor constante no tempo, representada pela função f, aquece a haste, então após um tempo suficientemente grande, a distribuição de temperatura u na haste pode ser descrita pela equação diferencial:

$$(\textbf{a}(x)\textbf{u}'(x))' = \textbf{f}(x), \ \ \ em \ \ \ (0,1),$$

juntamente com as condições de contorno

$$\textbf{u}(0) = \textbf{u}(1) = 0,$$

onde a função a representa a condutividade térmica da haste.

Do ponto de vista matemático, se as funções a e f pertencem a espaços vetoriais apropriados, pode-se então garantir que existe uma única função u (também pertencente a um espaço apropriado) satisfazendo a equação diferencial acima. Portanto, se a função f estiver fixada, pode-se definir o operador

$$F(\textbf{a}) = \textbf{u},$$

que a cada distribuição de condutividade térmica a, associa a distribuição de temperatura u correspondente. O problema inverso associado a essa equação consiste em reconstruir a condutividade térmica a da haste, através da medição aproximada da temperatura u.

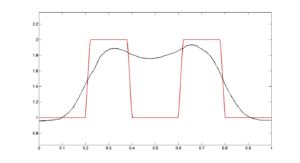
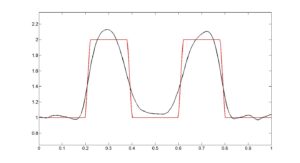
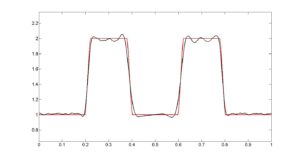
A figura abaixo apresenta as reconstruções a^δ (em azul) que aproximam a solução a (em vermelho) do problema inverso em questão, onde a fonte de calor f está fixada. Os resultados foram obtidos usando-se um método de regularização chamado de REGINN (REGularization based on INexact Newton iteration) com diferentes níveis de ruídos δ.