Impedance Tomography for monitoring multiphase flows

1. Introduction

Electrical Impedance Tomography (EIT) is a non-invasive procedure where electrodes are attached to the surface of an object and electrical currents are injected through them. The resulting voltages are then measured between pairs of electrodes. The purpose of the EIT is to use this information to build an image of the electrical conductivity of the interior of the studied object.

Recently, our team developed a complete system for EIT. This system articulates all the necessary steps for an EIT-type tomography, namely: it applies electrical currents and performs measurements of the corresponding potentials; from these data, it identifies (using a numerical analysis software) the electrical conductivity of the object under study.

Our next goal is building a complete system of Electrical Impedance Tomography (EIT) for monitoring multiphase flows.

 

This project is supported by CNPq (grant 406206/2021-0).

 

2. Description of the system in operation

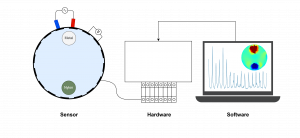
The system in operation consists of 3 main parts: sensor (data acquisition), hardware (data processing and digitalization) and software (conductivity identification using the data). A more detailed description of each of these parts follows:

Sensor

It is a plastic container with 16 stainless steel electrodes attached to the inside.

To carry out the experiments, we fill the plastic container with salt water and then we add some objects of different shapes, made for example, of steel or nylon.

Through the electrodes, we apply electrical current and measure the resulting electrical potential.

Hardware

It controls the amplitude of the electrical current applied to the electrodes, and measures the  resulting voltages.

After all the voltages between consecutive electrodes are recorded, the analog signal is converted into digital and a vector similar to the following is obtained:

This vector is now used to build an image of the electrical conductivity of the materials inside the container.

Software

It is an algorithm that solves the EIT inverse problem by applying a regularization technique. It uses the measurements of the electrical potential, informed by the hardware, and produces an image of the electrical conductivity.

Real image	Measured potencial	Conductivity reconstruction

The algorithm is coded in Python and is available on GitHub for free use in this link. Its documentation can be found here, and a detailed explanation (in Portuguese) of the computational implementation of this problem is available here.

 

3. Complete system of EIT for monitoring multiphase flows

 

We intend to improve the system described above, with three main objectives in mind:

a. Simultaneous reconstruction of images of electrical conductivity and permitivity;
b. Reconstruction of electrical conductivity images in real-time;
c. Determination of specific characteristics of multiphase flows, e.g., determination of the volumetric fraction and classification of flow patterns.

State of the art and limitations

The system currently in operation works satisfactorily on building images of electrical conductivity. However, the reconstruction of the electrical permittivity is not possible with this device. In addition, the measurement of voltages and the image reconstruction procedure are slow.

Main steps to be performed in the project

We want to build a new system, capable of collecting enough data to determine not only the electrical conductivity, but also the permittivity. In addition to these hardware improvements, a software update will be required to reconstruct functions with range in the set of complex numbers (simultaneous reconstruction of conductivity and permittivity).

To produce the images quickly and accurately, sophisticated regularization techniques will be required. We plan to adapt, improve or develop regularization methods to this end.

 

4. References

 

Below is a list of papers on this topic:

[18] Fábio Margotti, Eduardo Hafemann e Lucas Marcilio Santana. Implementação computacional da tomografia por impedância elétrica. Ed. do IMPA, Rio de Janeiro, 2023. ISBN: 978-85-244-0534-1 (print), 978-85-244-0535-8 (ebook).

[17] Fábio Margotti. Linear functional strategy and the approximate inverse for nonlinear ill-posed problems. Numerical Functional Analysis and Optimization, 44:10, 1060-1093, 2023.

[16] R. Filippozzi, E. Hafemann, J. Rabelo, F. Margotti. A. Leitão. A range-relaxed criteria for choosing the Lagrange multipliers in the Levenberg-Marquardt Kaczmarz method for solving systems of nonlinear ill-posed equations: Application to EIT-CEM with real data. Journal of Inverse and Ill-Posed Problems, 31(2):267-292, 2023.

[15] Fábio Margotti, Eduardo Hafemann. Range-relaxed strategy applied to the Levenberg-Marquardt method with uniformly convex penalization term in Banach spaces. Inverse Problems, 38 (2022) 095001 (35pp).

[14] R. Filippozzi, E. Hafemann, J. Rabelo, F. Margotti. A. Leitão. A range-relaxed criteria for choosing the Lagrange multipliers in the Levenberg-Marquardt Kaczmarz method for solving systems of nonlinear ill-posed equations: Application to EIT-CEM with real data. Journal of Inverse and Ill-Posed Problems. 2022. Accepted.

[13] A. Leitão, F. Margotti, B. Svaiter. Range-relaxed criteria for choosing the Lagrange multipliers in the Levenberg-Marquardt method. IMA Journal of Numerical Analysis, 2020. To appear.

[12] F. R. Moreira da Mota, D. J. Pagano and M. Enricone Stasiak. Water Volume Fraction Estimation in Two-Phase Flow Based on Electrical Capacitance Tomometry, in IEEE Sensors Journal, vol. 18, no. 16, pp. 6822-6835, 15 Aug.15, 2018.

[11] F. R. Moreira da Mota, D. J. Pagano and M. Enricone Stasiak. Development of a Tomometry Measurement Technique based on Electrical Capacitance Tomography and Combining Electrode Strategy, 8th World Congress on Industrial Process Tomography, 2016.

[10] F. Margotti. Mixed gradient-Tikhonov methods for solving nonlinear ill-posed problems in Banach spaces. Inverse Problems, 32(12):125012, 25pp, 2016.

[9] F. R. Moreira da Mota. Tomometria capacitiva aplicada à medição de fração de água em escoamentos bifásicos, tese de doutorado, Universidade Federal de St. Catarina, 2015.

[8] F. Margotti. On Inexact Newton Methods for Inverse Problems in Banach Spaces, tese de doutorado, Karlsruhe Institut für Technologie, 2015.

[7] F. Margotti, Andreas Rieder and Antonio Leitão. A Kaczmarz version of the REGINN-Landweber iteration for ill-posed problems in Banach spaces. SIAM J. Numer. Anal., 52(3):1439-1465, 2014.

[6] F. R. Moreira da Mota. Contribuições para o desenvolvimento de um sistema de medição multifásica com estágio de separação parcial. Dissertação de mestrado, Universidade Federal de St. Catarina, 2011.

[5] A. Leitão, B. Kaltenbacher, J. Baumeister. On Levenberg-Marquardt-Kaczmarz iterative methods for solving systems of nonlinear ill-posed equations, Inverse Problems and Imaging 4 (2010), no. 3, 335-350.

[4] A. Leitão, M. Haltmaier, R. Kowar, O. Scherzer. Regularization of systems of nonlinear ill-posed equations: II. Applications, Inverse Problems and Imaging 1 (2007) no. 3, 507-523.

[3] A. Leitão. Semiconductors and DtN maps, Computational and Applied Mathematics 25 (2006), no. 2-3, 187-203.

[2] A. Leitão, P. A. Markowich, J. P. Zubelli. On inverse dopping profile problems for the stationary voltage-current map, Inverse Problems 22 (2006), no. 3, 1071-1088.

[1] A. Leitão, M. Burger, H. W. Engl, P. A. Markowich. On inverse problems for semiconductor equations, Milan Journal of Mathematics 72 (2004), no. 1, 273-313.