Exemplo (operador integral)
No que se segue, descreveremos matematicamente um problema mal-posto. Esse é um exemplo técnico e sua compreensão exige conhecimentos prévios de análise.
Seja X = C[0,1] o espaço vetorial de todas as funções contínuas reais definidas no intervalo [0,1]. Equipe X com a norma infinito, definida por
$$\|f\| = \max_{x \in [0,1]}|f(x)|.$$
Então X é um espaço normado (até mesmo Banach). Defina Y = X e considere o operador integral, A:X→Y, definido por
$$(Af)(x) = \int_0^x f(s)ds, \ \ \ \ \ \ x \in [0,1].$$
Então A está bem-definido e é linear. Além disso, A é limitado pois
$$\|Af\| = \max_{x \in [0,1]}\big{|}(Af)(x)\big{|} = \max_{x \in [0,1]}\Big{|}\int_0^x f(s)ds \Big{|} \leq \max_{x \in [0,1]}\int_0^x |f(s)|ds,$$
ou seja,
$$\|Af\| \leq \max_{x \in [0,1]}\max_{t \in [0,1]}|f(t)|\int_0^x ds = \max_{x \in [0,1]}\|f\|(x - 0) =\|f\|, $$
o que prova que a norma de A é menor ou igual a 1. Além disso, A é injetiva, pois se f∈X e Af = 0, então, como f é contínua, segue do Teorema Fundamental do Cálculo que, para qualquer x∈[0,1],
$$\int_0^x f(s) = 0 \Longrightarrow \frac{d}{dx}\int_0^x f(s) = \frac{d}{dx}[0]\Longrightarrow f(x) = 0,$$
o que prova a afirmação. Então a primeira condição na definição de Hadamard é satisfeita. Vamos mostrar agora que a imagem de A é o conjunto
$$Z = \{g \in C^1[0,1]: g(0) = 0\}.$$
De fato, se g pertence à imagem de A, então existe uma função contínua f tal que Af = g, ou seja, g é a integral de uma função contínua e portanto é continuamente diferenciável. Além disso, segue diretamente da definição de A que g(0) = (Af)(0) = 0. Assim, g∈Z. Por outro lado, se g∈Z, então a função f = g' é contínua e para todo x∈[0,1] vale
$$(Af)(x) = \int_0^x f(s)ds = \int_0^x g'(s)ds = g(x),$$
ou seja, g pertence à imagem de A, o que prova a afirmação. Como Z≠Y, o operador A não é sobrejetivo e portanto a segunda condição na definição de Hadamard não é satisfeita, o que prova que esse problema é mal-posto.
Vamos fazer agora uma pequena mudança nos espaços onde o operador A age, substituindo Y por Z. Então o novo operador A:X→Z, continua operando entre espaços vetoriais normados, está bem-definido, é linear, contínuo e injetivo. Além disso, A é agora sobrejetivo também e portanto inversível. As duas primeiras condições na definição de Hadamard são portanto satisfeitas para A. Observe que a inversa de A é o operador de derivação. Vamos provar que A-1 é descontínua.
Com efeito, seja f a função constante nula e defina a sequência de funções (fk)⊂X por
$$f_k (x) = k\cos (k^2 x), \ \ \ \ \ x \in [0,1].$$
Então
$$(Af_k)(x) = \int_0^x f_k(s)ds = \int_0^x k\cos (k^2 s)ds = \frac{\sin (k^2 x)}{k}.$$
Portanto,
$$\|Af_k - Af\| = \|Af_k\| = \max_{x \in [0,1]} \big{|}(Af_k)(x)\big{|} = \frac{1}{k}\max_{x \in [0,1]} |\sin (k^2 x)| \leq \frac{1}{k}.$$
Conclui-se que
$$Af_k \longrightarrow Af, \ \ \ \ \text{quando} \ \ \ \ k \longrightarrow \infty.$$
Mas, ao mesmo tempo, (fk) não converge a f, pois
$$\|f_k - f\| = \|f_k\| = \max_{x \in [0,1]} \big{|}(f_k)(x)\big{|} = k\max_{x \in [0,1]} |\cos (k^2 x)| = k \longrightarrow \infty, \ \ \ \ \text{quando} \ \ \ \ k \longrightarrow \infty.$$
Isso mostra que a solução do problema inverso não depende continuamente dos dados. Logo, a terceira condição na definição de Hadamard não é satisfeita e portanto o problema inverso em questão é mal-posto.
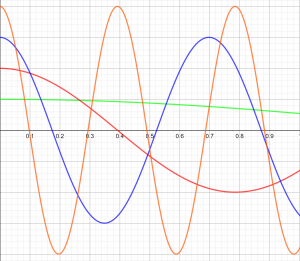 |
 |
f1, f2, f3 e f4 em verde, vermelho, azul elaranja, respectivamente. (fk) não converge. |
Af1, Af2, Af3 e Af4 em verde, vermelho, azul elaranja, respectivamente. (Afk) converge a zero. |
Esse exemplo ilustra o fato de que o problema de recuperar uma função contínua a partir de sua integral (ou equivalentemente, de derivar uma função continuamente diferenciável) é um procedimento instável.




